ฟังก์ชันค่าสัมบูรณ์

ฟังก์ชันค่าสัมบูรณ์ฟังก์ชันค่าสัมบูรณ์ คือ ฟังก์ชันที่อยู่ในรูปy = |x - a| + c เมื่อ a และ c เป็นจำนวนจริงฟังก์ชันค่าสัมบูรณ์กราฟของฟังก์ชันค่าสัมบูรณ์ จะมีลักษณะเป็นเส้นตรงสองเส้นมาเจอกันที่จุดหักมุมฟังก์ชันค่าสัมบูรณ์เมื่อหน้าค่าสัมบูรณ์มีค่า + จะได้กราฟหงาย อ่านต่อ

ฟังก์ชันเชิงเส้น

ฟังก์ชันเชิงเส้น   คือ ฟังก์ชันที่อยู่ในรูป y = ax+b เมื่อ a ,b เป็นจำนวนจริง และ  กราฟของฟังก์ชันเชิงเส้นจะเป็นเส้นตรง อ่านต่อ

บทที่4 ความสำพันธ์และฟังก์ชัน

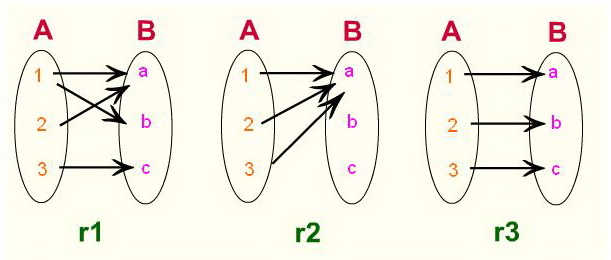
1)คู่อันดับ : เขียนคู่อันดับในรูป (a,b) โดยที่  a เป็นสมาชิกตัวหน้า และ  b เป็นสมาชิกตัวคู่หลัง คู่อันดับสองคู่อันดับใดๆ จะเท่ากัน ก็ต่อเมื่อสมาชิกตัวหน้าและสมาชิกตัวหลังของทั้งสองคู่อันดับนี้เท่านั้น2) ผลคูณคาร์ทีเซียน : ผลคูณคสร์ทีเซียนของเซต A และ B เขียนแทนด้วย A x  B  หมายถึง เซตของคู่อันดับ (X , Y )  ทั้งหมด โดยที่  X   เป็นสมาชิกเซต A และ Y เป็นสมาชิกของเซต B อ่านต่อ

การนำสมบัติของจำนวนจริงไปใช้ในการแก้สมการกำลังสอง

การนำสมบัติของจำนวนจริงไปใช้ในการแก้สมการกำลังสองตัวแปร : อักษรภาษาอังกฤษตัวเล็ก เช่น x , y ที่ใช้เป็นสัญลักษณ์แทนจำนวนค่าคงตัว : ตัวเลขที่แททนจำนวน เช่น 1, 2
นิพจน์ : ข้อความในรูปสัญลักษณื เช่น 2, 3x ,x-8 , อ่านต่อ

สมบัติของจํานวนจริงเกี่ยวกับการบวกและการคูณ

 จำนวนตรรกยะ (rational number) เป็นจำนวนจริงที่สามารถเขียนได้ในรูปเศษส่วนของจำนวนเต็มที่ตัวส่วนไม่เป็นศูนย์  และเขียนในรูปทศนิยมซ้ำได้จำนวนอตรรกยะ (irrational number)  เป็นจำนวนจริงที่ไม่ใช่จำนวนตรรกยะซึ่งไม่สามารถเขียนในรูปทศนิยมซ้ำหรือเศษส่วนของจำนวนเต็มที่ตัวส่วนไม่เป็นศูนย์แต่เขียนได้ในรูปทศนิยมไม่ซ้ำอ่านต่อ

บที่3 จำนวนจริง

เซตของจำนวนจริงประกอบด้วยสับเซตที่สำคัญ  ได้แก่  เซตของจำนวนนับ/ เซตของจำนวนเต็มบวก เขียนแทนด้วย  II = {1,2,3…}เซตของจำนวนเต็มลบเขียนแทนด้วยIเซตของจำนวนเต็ม เขียนแทนด้วย I
I = { …,-3,-2,-1,0,1,2,3…}เซตของจำนวนตรรกยะ : เซตของจำนวนจริงที่สามารถเขียนได้ในรูปเศษส่วน โดยที่ a,b เป็นจำนวนเต็ม  และ b = 0 อ่านต่อ

บทที่2 การไห้เหตุผล

การให้เหตุผลทางคณิตศาสตร์ที่สำคัญมีอยู่ 2 วิธี คือ1การให้เหตุผลแบบอุปนัยเป็นการสรุปผลในการค้นหาความจริงจากการสังเกต  หรือการทดลองหลายครั้งจากกรณีย่อยๆ แล้วนำมาสรุปเป็นความรู้แบบทั่วไป ซึ่งข้อสรุปที่ไม่จำเป็นต้องถูกต้องทุกครั้ง 2การให้เหตุผลแบบนิรนัย เป็นการนำสิ่งที่ยอมรับว่าเป็นจริงมาประกอบเพื่อนำไปสู่ข้อสรุปจากสิ่งที่ยอมรับแล้วอ่านต่อ

สับเซตและเพาเวอร์เซต

ถ้าสมาชิกทุกตัวของ A เป็นสมาชิกของ B แล้ว จะเรียกว่า A เป็นสับเซตของ B จะเขียนว่า
เซต A เป็นสับเซตของเซต B แทนด้วย A ⊂ B ถ้าสมาชิกบางตัวของ A ไม่เป็นสมาชิกของ B จะเรียกว่า A ไม่เป็นสับเซตของ Bเซต A ไม่เป็นสับเซตของเซต B แทนด้วย A ⊄ B อ่านต่อ

เอกภพสัมพัทธ์

เอกภพสัมพัทธ์ คือ เซตที่กำหนดขอบเขตของสิ่งที่ต้องการศึกษา ซึ่งถือว่าเป็นเซตที่ใหญ่ที่สุด โดยมีข้อตกลงว่า ต่อไปจะกล่าวถึงสมาชิกของเซตนี้เท่านั้น จะไม่มีการกล่าวถึงสิ่งใดที่นอกเหนือไปจากสมาชิกของเซตที่กำหนดขึ้นนี้ โดยทั่วไปนิยมใช้สัญลักษณ์ U แทนเอกภพสัมพัทธ์ อ่านต่อ

บทที่1 เซต

เซต เป็นคำที่ใช้บ่งบอกถึงกลุ่มของสิ่งต่างๆ และเมื่อกล่าวถึงกลุ่มใดแน่นอนว่าสิ่งใดอยู่ในกลุ่ม สิ่งใดไม่อยู่ในกลุ่ม เช่นเซตสระในภาษาอังกฤษ  หมายถึง  กลุ่มของอังกฤษ  a, e, i, o และ u เซตของจำนวนนับที่น้อยกว่า 10 หมายถึง  กลุ่มตัวเลข 1,2,3,4,5,6,7,8,และ9 อ่านต่อ